Deitel_Java_7.23 a) ( Circuito del Caballo en Java, Método de Fuerza Bruta)

Una solución al recorrido del caballo

7.23 (Paseo del Caballo: Métodos de Fuerza Bruta) En la parte c del ejercicio 7.22 desarrollamos una solución al problema del paseo del caballo. El método utilizado, llamado "heurística de accesibilidad", genera muchas soluciones y se ejecuta con eficiencia. A medida que se incremente de manera continua la potencia de las computadoras, seremos capaces de resolver más problemas con menos potencia y algoritmos relativamente menos sofisticados. A éste le podemos llamar el método de la "fuerza bruta" para resolver problemas.

a) Utilice la generación de números aleatorios para permitir que el caballo se desplace a lo largo del tablero (mediante sus movimientos legítimos en L) en forma aleatoria. Su aplicación debe ejecutar un paseo e imprimir el tablero final. ¿Qué tan lejos llegó el caballo?
_____________________________________________________________________________________
SOLUCIÓN:
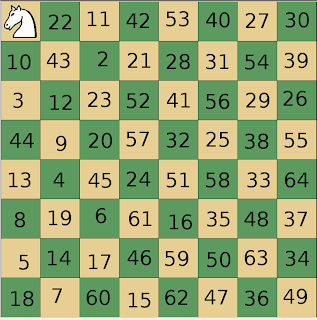
En este programa el caballo llega tan lejos como el usuario quiera. Se ha puesto un ciclo while que corre el algoritmo tantas veces como sean necesarias para que se obtengan las casillas deseadas. En los comentarios del programa viene bien explicado de qué se trata. Pero debo decir que este algoritmo es bastante simple. La clase Caballo, que es la que hace el trabajo, tiene, con comentarios, 176 líneas de código. He visto soluciones más complicadas, y yo mismo tengo en este blog unas muy rebuscadas. La idea es muy sencilla. El caballo empieza en una casilla la (1,1) en este caso pero puede ser cualquiera, a partir de ahí ¿a dónde mover? Ya que el problema va a ser resuelto mediante la fuerza bruta suponemos que un mono lanza un par de dados que tienen caras del 1 al 8. El primero de ellos decide la linea y el siguiente la columna. Si antes no ha pasado el caballo por ahí, lo cual se indica con un numero, entonces el mono procede a medir la distancia entre la posicion actual en x y la coordenada x de la casilla, si es 1 o 2 se analiza la distancia en y, la cual debe ser 2 o 1, respectivamente. Si se cumplen estas condiciones entonces se escribe el número de casillas que lleva recorridas el caballo y se sigue adelante. El caballo puede llegar a un punto muerto. Si después de un cierto número de lanzamientos de dados (1000 en este programa) no se ha incrementado el número de casillas recorridas, entonces se deja de intentar. El programa pregunta cuántas casillas quiere que recorra el caballo. Es bueno iniciar con pocas, pero en realidad la única que tarda un poco ( unos cinco minutos en promedio en mi máquina bastante vieja ) es 64. El recorrido de la figura fue obtenido en unos dos minutos aproximadamente.
Más importante aún, con cambiar 8 por cualquier otro número se puede encontrar recorridos para tableros de nxn y resolver el problema general. En teoría de grafos este problema consiste en encontrar el circuito de Hamilton, aquel que pasa por todas las aristas del grafo.

Este código debe guardarse con el nombre UsaCaballo.java

public class UsaCaballo

{  // Abre  UsaCaballo

public static void main(String args[])
{     // Abre main
Caballo miObjeto = new Caballo();
miObjeto.Recibe();
}     // Cierra main

}  // Cierra UsaCaballo

El siguiente código debe guardarse con el nombre Caballo.java

/*+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
  *                                                                        *
  *                                                                        *
  *                            DEITEL 7.23 a)                              *
  *                                                                        *
  *  Este programa intenta el recorrido del caballo en un tablero de       *
  *  ajedrez mediante la fuerza bruta.                                     *
  *                                                                        *
  *                                                                        *
  *++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++*/

  /*++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
   *                                                                       *
   *                               ALGORITMO:                              * 
   *                               __________                              *
   *                                                                       * 
   *  La idea de este algorimo es bastante simple:                         *
   *                                                                       *
   * PASO 1: El tablero de ajedrez (arreglo de 8x8) se llena con 0 en todas*
   * las entradas exepto en la esquina superior derecha, que se coloca un 1*
   * De ahi es de donde parte el caballo.                                  *
   *                                                                       *  
   * PASO 2: Se lanza un par de "dados" de ocho caras El primer dado decide*
   * el renglon, el siguiente decide la columna.                           *
   *                                                                       *
   *PASO 3: Es necesario verificar que el caballo no haya pasado antes por *
   *ahi, o que la casilla seleccionada tenga un 0 Si no es asi se repite el*
   *Paso2. Si efectivamente es un 0, entonces se verifica que la casilla   *
   *elegida al azar sea "legal" o este en forma de L Para esto se verifican*
   *las distancias en X y en Y. Si el valor absoluto de la diferencia entre*
   *la casilla elegida por el dado1 y la casilla x actual es igual a 2 o  1*
   *se procede a checar el valor absoluto de la distancia entre dado2 y Y. *
   *1 para el primer caso y 2 para el segundo, indican que la casilla es   *
   *valida. Se procede a poner el numero  2 ( o 3 o 4 o el que sea)  en la *
   *casilla, lo cual indica que esa es la siguiente parada del caballo. Se *
   *incrementa la variable contador y se procede de esa manera.            * 
   *                                                                       * 
   *                                                                       *  
   *Eso es todo. Esa es la idea central. Lo demas consiste en decirle al   *
   *programa cuando ya no es posible encontrar mas casillas, y por lo      * 
   *tanto se ha llegado a un rincon sin salida. Para eso se introduce una  *
   *variable que cuenta el numero de veces que se ha lanzado los dos dados *
   *sin cambiar de casilla.  Si se cumplen estos el programa entiende que  *
   *no hay salida y deja de intentar buscarla. Esto significa que 15 de    *
   *cada 1000 veces dejara de intentar cuando en realidad hay una casilla  *
   *a la cual mover. Se puede cambiar y poner un limite mas grande, pero   *
   *como he puesto un ciclo mas grande afuera que permite al usuario pedir *
   *una cuota minima de recorrido, hacerlo significa mas tiempo.           *
   *                                                                       *
   *                                                                       *
   *+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++*/

import java.util.Scanner;
import java.util.Random;

public class Caballo
{  // Abre clase Caballo
private int x = 1;  // El caballo inicia en la casilla superior izquierda
private int y = 1;
private int tamano = 8; // El arreglo es de ocho x ocho
private int contador = 1; // Esta variable lleva la cuenta de las casillas
                           // recorridas
int ciclos = 0;           // Esta variable cuenta los ciclos que se inten
                           // tan antes de determinar que ya no hay lugares
                           // a los cuales ir                            
int intentos_fallidos = 0; // Esta variable cuenta cuantos ciclos se inte
  //tan antes de obtener el que pidio el usuario para 64 pueden ser varios
  // millones

Scanner entrada = new Scanner(System.in);
 
public void Recibe() 
{  // Abre Recibe
Random aleatorio = new Random();

int Arreglo[][] = new int[tamano + 1][tamano +1];
// Se define el arreglo de 9*9 para evitar el 0 
Arreglo[1][1] = 1;
int dado1;
int dado2;
int casillas_requeridas = 0;
  
System.out.println("\nCuantas casillas quiere que recorra por lo menos?");
System.out.printf("\nAdvertencia: Si pide mas de %d el programa no terminara nunca:\n", tamano*tamano);
  casillas_requeridas = entrada.nextInt();
  
// Debido a que se usara la fuerza bruta de la computacion para encontrar un
// recorrido completo se anade este while

while ( contador < casillas_requeridas )
{
intentos_fallidos++;  // Se incrementa cada que inicia un intento
contador = 1;    // Dado que ya se ha colocado al caballo en (1,1), se  
                   // inicia el contador en 1
int ciclos = 0;   // Se inicia con 0 ciclos o lanzamientos de dados infructuosos 
// Cada vez que se aborta un intento han de limipiarse las casillas, con el siguiente
//par de ciclos se establecen a 0 nuevamente.

for ( int s = 0; s <= tamano; s++ )
{       // Abre for
for ( int t = 0; t <= tamano; t++ )
Arreglo[s][t] = 0; 
}       // cierra for 
 
//Se ha de colocar el caballo en la esquina superior izquierda cada vez
// desde luego se puede poner en cualquier parte
x = 1;
y = 1;
 
Arreglo[1][1] = 1;
// Mientras no se encuentre un lugar para poner al caballo

while ( 1000 != ciclos)
// Este ciclo while basicamente hace el PASO 3 del algoritmo
{  // Abre while
ciclos++;
dado1 = 1 + aleatorio.nextInt(8);
dado2 = 1 + aleatorio.nextInt(8);

if ( Math.abs(Math.abs(x) - Math.abs(dado1)) == 2) 
{ // Abre if
if ( Math.abs(Math.abs(y) - Math.abs(dado2)) == 1  )
 
if ( 0 == Arreglo[dado1][dado2])
{   // Abre if
Arreglo[dado1][dado2] = ++contador;   
x = dado1;
y = dado2;
ciclos = 0;
}  // Cierra if 
}  //Cierra if 

 
if ( Math.abs(Math.abs(x) - Math.abs(dado1)) == 1) 
{  // abre if
if ( Math.abs(Math.abs(y) - Math.abs(dado2)) == 2  )
if ( 0 == Arreglo[dado1][dado2] )
{    // Abre if 
Arreglo[dado1][dado2] = ++contador; 
x = dado1;
y = dado2;
ciclos = 0;
}  // Cierra if
}  // Cierra if
 
}  // Cierra while anidado
}    // Cierra while

System.out.println("\nLISTO!");
System.out.printf("\nSe recorrieron %d casillas.\n", contador);
System.out.printf("\nSe intentaron %d circuitos antes de obtener el requerido.\n", intentos_fallidos); 
Imprime( Arreglo );

}   // Cierra Recibe

/*El metodo siguiente despliega el tablero de ajedrez */

//////////////////////////////////////////
// Imprime
///////////////////////////////////////////
 
public void Imprime(int B[][])
{     // Abre imprime
for ( int k = 1; k <= 8; k++ )
{
for ( int j = 1; j <= 8; j++)
{
System.out.printf("%5d", B[k][j]);
 
}  
System.out.println("\n");
}
}     // Cierra imprime
}    // Cierra clase Caballo