Kernighan_Ritchie_2.6 (Desplazamiento y sustitución de bits)

_______________________________________________________________________________________
2.6 Escriba una función setbits(x,p,n,y) que regresa x con los n bits que principian en la posición p iguales a los n bits más a la derecha de y, dejando los otros bits sin cambio.
_______________________________________________________________________________________
Solución:
Lo primero, igual que en este ejemplo, es entender bien el enunciado. Para ésto, vamos a visualizar la representación binaria de un par de números enteros positivos, digamos el 51 y el 42. Para estos números bastan seis bits. Vamos a suponer que el número de bits del primer entero (51) que vamos a cambiar por otros tantos del segundo (42) serán 3 (la variable n de setbits), y que además queremos cambiarlos a partir de la posición 1 (variable p ). Es importante recordar que la posición extrema derecha de un byte es el bit 0. Una vez establecido ésto, lo que el programa quiere es lo que se muestra en la siguiente figura:

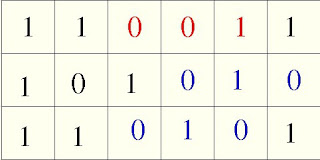La función setbits elimina los bits rojos y los sustituye por los azules.

La función setbits intercambia los 3 bits a partir del primero en la representación binaria de 51, con los tres primeros de la representación binaria de 42. El resultado es el número 53. Una vez entendida esta gráfica, es muy fácil entender la línea única de la función:

return (~((~0 << p) & ~(~0 <<(p+n))) & x ) | (~(~0 << p+n) & (y << p));

Esta línea, a pesar de parecer muy poco intuitiva, surge de una análisis simple.
1) Hacer 0 los bits entre p y p+n en el primer número. Ésto se logra creando una máscara que contenga 1s en todas las entradas, salvo en dichos bits. Esa máscara se crea con (~((~0 << p) & ~(~0 <<(p+n))) & x ). 2) Correr los bits del segundo número hasta la posición p. Ésto es, (y << p). 3) Hacer 0 los bits del segundo número, salvo en los intervalos 0-p y p+n hasta el último. Esto se logra con la máscara (~(~0 << p+n) & (y << p)). 4) Usar el operador | para lograr la unión de los bits distintos de 0 en de ambos números.
En los comentarios del programa se presenta éste mismo procedimiento como explicación del algoritmo.

/*+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++*
* Este programa recibe dos enteros sin signo. Regresa otro entero sin    *
* signo, el que se obtiene al cambiar n bits del primero, a partir de la *
* posicion p, con los n bits mas a la derecha del segundo.               *
*                                                                        *
* Lo que recibe: 4 enteros positivos.                                    *
* Lo que regresa: 1 entero positivo.                                     *
*++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++*/

/*++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
*                               ALGORITMO:                               *
*Establecer a o los n bits del primer numero, a partir de la posicion p  *
*                                                                        *
*                                              p                         *
*      | x | x | x | x | x | x | 0 | 0 | ... | 0 | x | x | x |           *
*                              -     n   --------                        *
*                                                                        * 
*Mover los bits del segundo numero p posiciones a la izquierda           *
*                                                                        *
*Establecer a 0 todos los bits (antes de la posicion p y despues de la n)*
*del segundo numero                                                      *
*                                                                        *
*                                  n             p                       *
*      | 0 | 0 | 0 | 0 | ... | 0 | x | x | ... | x | 0 | 0 | 0 |         *
*                                                                        *
*Con el operador o inclusivo | (puede ser el ^ o exclusivo) obtener el   *
*numero buscado.                                                         *
*++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++*/

#include 

///////////////////////////////////////////////////////////////////////
//setbits
///////////////////////////////////////////////////////////////////////

unsigned setbits( unsigned x, int p, int n, unsigned y)
{ /* Abre setbits */
 return (~((~0 << p) & ~(~0 <<(p+n))) & x ) | (~(~0 << p+n) & (y << p));
} /*Cierra setbits */

///////////////////////////////////////////////////////////////////////
//MAIN
///////////////////////////////////////////////////////////////////////

int main()
{  /* Abre main */
unsigned numero1, numero2;
int a, b;

printf("\nIntroduzca un entero sin signo: ");
scanf("%d", &numero1);

printf("\nIntroduzca un segundo entero sin signo: ");
scanf("%d", &numero2);

printf("\nIntroduzca el numero de bits a cambiar: ");
scanf("%d", &a);

printf("\nIntroduzca el bit a partir del cual se hara el cambio: ");
scanf("%d", &b);

printf("\nEl numero resultante es: %d\n", setbits(numero1, b, a, numero2));  

return 0; 
}  /* Cierra main */

ÉSte programa no tiene la precaución de verificar que los valores sean válidos. Por ejemplo, se podría introducir un valor de p mayor que el número total de bits. Ésto se puede evitar colocando algunos condicionales en la función main. No he querido colocarlos para no complicar el código. Es fácil hacerlo.
Aquí una ejecución, usando los números presentados anteriormente.

[hernandez@localhost Programas]$ ./a.out 

Introduzca un entero sin signo: 51

Introduzca un segundo entero sin signo: 42

Introduzca el numero de bits a cambiar: 3

Introduzca el bit a partir del cual se hara el cambio: 1

El numero resultante es: 53

__________________________________________________________________________________________
Esta entrada es parte de los problemas resueltos del libro El Lenguaje de Programación C de B. Kernighan y D. Ritchie
Entrada Anterior

Un ejemplo usando operadores para manejo de bits

Éste programa usa la función getbits (sección 2.9 de El Lenguaje de Programación C, de Kernighan y Ritchie). La razón para ponerlo aquí es que no es claro a primera vista, al menos para mí, lo que esa función hace. En la sección 2.9 se estudian los operadores binarios y getbits hace uso de &, el and de bits; <<, corrimiento a la izquierda; >>, corrimiento a la derecha y ~, complemento a uno, para hacer lo siguiente:

"regresa el campo de n bits de x (ajustado a la derecha) que principia en la posición p. Se supone que la posición del bit 0 está en el borde derecho y que n y p son valores positivos adecuados. Por ejemplo, getbits(x,4,3) regresa los tres bits que están en la posición 4, 3 y 2 ajustados a la derecha."

No soy el único que encuentra difícil la redacción (la original, en inglés) del libro de Kernighan y Ritchie. He encontrado varias páginas y foros en los que la gente se pregunta qué quisieron decir en tal o caul parte. Afortunadamente, aquí se puede entender sin ambigûedades.
Vamos a suponer que las variables son éstas: x = 179, p = 4 y n = 3. Para hacer ésto más fácil, la representación binaria de 179 es la siguiente:

Representación binaria de 179, en 10 bits.

Lo que hace nuestra función es mostrar dejar únicamente los 3 bits que comienzan a partir de la posición 4 (la posición extrema derecha es la 0). Éstos bits son 1 0 0, y deben aparecer corridos hacia la derecha. Todos los demás bits deben estar establecidos en 0.

El número 179 después de aplicar getbits.

El corazón del programa es, desde luego, la instrucción

return ((x >> (p+1-n)) & ~(~0 << n));

Ésta línea se divide en dos partes, separadas por el operador &. La instrucción x >> (p+1-n) corre hacia la derecha (4+1-3 = 2) bits. Esto es, se eliminan los bits 0 y 1 (ambos con 1), que deja el número binario 0000101100.
~(~0 << n) crea una máscara de bits. ~0 genera el binario 1111111111 y ~0 << n, con n = 3, corre hacia la izquierda el primer bit y llena los espacios con 0. Se produce entonces el número binario 1111111000. Finalmente, ~(~0 << n) crea el binario 0000000111. Esta es la máscara. Aplicando el operador & a 0000101100 y 0000000111 produce 0000000100. Este número es 4. Es precisamente lo que se obtiene al ejecutar el programa

/*++++++++++++++++++++++++++++++++++++++++++++
 * "regresa el campo de n bits de x (ajustado *
 * a la derecha) que principia en la posicion *
 * p. Se supone que la posicion del bit 0     *
 * esta en el borde derecho y que n y p son   *
 * valores positivos adecuados" Kernighan-    *
 * Ritchie                                    *
 *+++++++++++++++++++++++++++++++++++++++++++*/
#include 

///////////////////////////////////////
// FUNCION GETBITS
// ////////////////////////////////////

unsigned getbits(unsigned x, int p, int n)
{ /* Abre getbits*/
 
return ((x >> (p+1-n)) & ~(~0 << n));

} /*Cierra getbits*/

////////////////////////////////////////
//FUNCION MAIN
////////////////////////////////////////

int main()
{ /* Abre main*/

unsigned numero;
int a, b;

printf("\nIntroduzca un entero sin signo: ");
scanf("%d", &numero);

printf("\nIntroduzca el numero de bits a mostrar: ");
scanf("%d", &b);

printf("\nIntroduzca el numero de bit a partir del cual se mostraran: ");
scanf("%d", &a);

printf("El numero es: %d\n", getbits(numero,a,b));

return 0;
}/*Cierra main*/

Aquí la ejecución

[hernandez@localhost Programas]$ ./a.out 

Introduzca un entero sin signo: 179

Introduzca el numero de bits a mostrar: 3

Introduzca el numero de bit a partir del cual se mostraran: 4
El numero es: 4

De decimal a octal con una función recursiva

Éste programa es una consecuencia natural de la entrada anterior. Es tan simple como cambiar 2 por 8. En realidad, como puede verse, éste procedimiento sirve para convertir de decimal a cualquier base posicional entre 2 y 9. También es posible usarlo para una conversión a sistema hexadecimal.

#include <stdio.h>

/*////////////////////////////////////
 * Funcion Octal                     *
 *///////////////////////////////////*/

void Octal( int x)

{  /* Abre Octal*/
if ( x != 0 )
{ /* Abre if*/
Octal(x/8);

printf("%d\t", x%8);
} /*Cierra if */

else;
 /*printf("0\n");*/

}  /*Cierra Octal*/

/****************************************
 * main                                 *
 ***************************************/
int main()

{  /*Abre main */
 int num; 

 printf("\nIntroduzca un numero entero: ");
 scanf("%d", &num);

 Octal(num);
 printf("\n");

 return 0;
}  /*Cierra main */

Y aquí una ejecución, con el número 100 como entrada

[hernandez@localhost Programas]$ ./a.out 

Introduzca un numero entero: 100                                                     
1       4       4                   

De decimal a binario con una función recursiva

Tengo una versión de éste programa que es bastante más complicada, pero por mucho tiempo recordé que lo había visto resuelto usando recursión. Ahora he pensado algunas formas de hacerlo, por ejemplo ésta:
Supongamos que tenemos el número 41, y que queremos convertirlo de su notación decimal a binario.

41 En binario  = 1 0 0 0 0 0 + (41 - 32) En binario

                                   9 En binario = 1 0 0 0 +  (9 - 8) En binario

                                                                1 En binario = 1.

El problema se va reduciendo cada vez por medio de llamadas a sí mismo con argumentos más simples. Al final sólo es necesario sumar las representaciones binarias de 32 + 8 + 1. Sin embargo no es ésto lo que yo quiero aquí. Además, sumar será en éste caso más complicado que la propia conversión. Por lo tanto descarté ésta posibilidad.
Otra forma es sugerida por el siguiente proceso, que puede encontrarse por ejemplo en el libro de Diseño Digital, de Morris Mano:

Número          División       Residuo          Binario
  41/2     =       40/2    +     1/2              1
  
  20/2     =       20/2    +      0               0

  10/2     =       10/2    +      0               0
 
   5/2     =        4/2    +     1/2              1
 
   2/2     =        2/2    +      0               0

   1/2     =          0    +     1/2              1

Éste algoritmo es fácilmente programable usando el operador %. Sin embargo, tiene el gran inconveniente de que los dígitos se imprimen en el orden inverso, como puede verse al ejecutar el siguiente código

#include <stdio.h>

/*////////////////////////////////////
 * Funcion Binario                   *
 *///////////////////////////////////*/

void Binario( int x)

{  /* Abre binario*/
if ( x != 0 )
{ /* Abre if*/
printf("%d\t", x%2);

Binario(x/2);

} /*Cierra if */

else;
 /*printf("0\n");*/

}  /*Cierra binario*/

/****************************************
 * main                                 *
 ***************************************/
int main()

{  /*Abre main */
 int num; 

 printf("\nIntroduzca un numero entero: ");
 scanf("%d", &num);

 Binario(num);

 return 0;
}  /*Cierra main */

La ejecución es la siguiente

[hernandez@localhost Programas]$ ./a.out 

Introduzca un numero entero: 41
1       0       0       1       0       1  

De nuevo el problema es que se está imprimiendo el número al revés. Ésto es grave, porque el código es muy bueno, y cualquier intento por corregir el defecto, requiere algoritmos más complicados que la propia conversión.
Sin embargo, después de pensarle, la solución es muy simple. En la función Binario, basta con cambiar el orden de los dos únicos enunciados. Primero hay que hacer una llamada a Binario, y ésto llevará la ejecución hasta el final, hasta el caso más simple, y el control se regresará desde el último caso, imprimiendo los dígitos binarios en el orden inverso. El programa correcto es el siguiente:

#include <stdio.h>

/*////////////////////////////////////
 * Funcion Binario                   *
 *///////////////////////////////////*/

void Binario( int x)

{  /* Abre binario*/
if ( x != 0 )
{ /* Abre if*/
Binario(x/2);

printf("%d\t", x%2);
} /*Cierra if */

else;
 /*printf("0\n");*/

}  /*Cierra binario*/

/****************************************
 * main                                 *
 ***************************************/
int main()

{  /*Abre main */
 int num; 

 printf("\nIntroduzca un numero entero: ");
 scanf("%d", &num);

 Binario(num);

 return 0;
}  /*Cierra main */

La ejecución,

[hernandez@localhost Programas]$ ./a.out 

Introduzca un numero entero: 41
1       0       1       0       0       1

Comopuede verse, son muy pocas las líneas que se requieren para hacer la conversión de binario a decimal usando la recursión, y es un cambio mínimo el que hace esta diferencia.